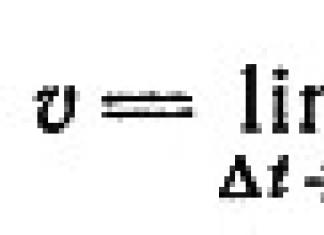La procedura che abbiamo appena seguito è così comune in matematica che è stata inventata una notazione speciale per le quantità ε e x: ε è indicato con ∆t e x con ∆s. Il valore di ∆t significa "piccole aggiunte a t", e si comprende che questa aggiunta può essere ridotta. Il simbolo ∆ in nessun caso significa moltiplicazione per un valore, così come sin θ non significa s i n 0. Questa è solo un'aggiunta al tempo, con il simbolo ∆ che ci ricorda il suo carattere speciale. Ebbene, se ∆ non è un fattore, allora non può essere ridotto rispetto a ∆s/∆t. È come nell'espressione sin θ/sin 2θ tagliare tutte le lettere e ottenere 1/2. In queste nuove notazioni, la velocità è uguale al limite del rapporto ∆s/∆t poiché ∆t tende a zero, cioè

Questa è essenzialmente la formula (8.3), ma ora è più chiaro che qui cambia tutto e, inoltre, ti ricorda esattamente quali quantità cambiano.
C'è un'altra legge che vale con buona precisione. Dice: la variazione della distanza è uguale alla velocità moltiplicata per l'intervallo di tempo durante il quale si è verificata questa variazione, ovvero ∆s = υ∆t. Questa regola è strettamente valida solo quando la velocità non cambia durante l'intervallo ∆t, e questo, in generale, avviene solo quando ∆t è sufficientemente piccolo. In questi casi si scrive solitamente ds = υdt, dove dt indica l'intervallo di tempo ∆t, purché arbitrariamente piccolo. Se l'intervallo ∆t è sufficientemente grande, la velocità può cambiare durante questo tempo e l'espressione ∆s = υ∆t sarà già approssimativa. Tuttavia, se scriviamo dt, allora questo implica che l'intervallo di tempo è infinitamente piccolo, e in questo senso l'espressione ds = υdt è esatta. Nella nuova notazione, l'espressione (8.5) ha la forma

La quantità ds/dt è detta "derivata di s rispetto a t" (tale nome ricorda ciò che sta cambiando), e viene anche chiamato il complesso processo di ricerca della derivata; differenziazione. Se ds e dt appaiono separatamente e non come un rapporto ds/dt, vengono chiamati differenziali. Per meglio informarti sulla nuova terminologia, dirò anche che nel paragrafo precedente abbiamo trovato la derivata della funzione 5t 2 , o semplicemente la derivata di 5t 2 . Si è rivelato essere pari a 10 t. Man mano che ti abituerai alle nuove parole, il pensiero stesso ti diventerà più chiaro. Per pratica, troviamo la derivata di una funzione più complessa. Si consideri l'espressione s = At ​​3 + Bt + C, che può descrivere il movimento di un punto. Le lettere A, B, C, così come nella consueta equazione quadratica, denotano numeri costanti. Abbiamo bisogno di trovare la velocità di movimento descritta da questa formula in ogni momento t. Per questo, considera il momento t + ∆t, e aggiungi qualche addizione ∆s a s, e trova come ∆s è espresso in termini di ∆t. Nella misura in cui

Ma non abbiamo bisogno del valore di ∆s stesso, ma del rapporto ∆s/∆t. Dopo aver diviso per ∆t, otteniamo l'espressione

che, dopo che ∆t tende a zero, si trasformerà in

Questo è il processo di assunzione di una derivata, o funzioni di differenziazione. In effetti, è un po' più facile di quanto sembri a prima vista. Si noti che se in espansioni come le precedenti ci sono termini proporzionali a (∆t) 2 o (∆t) 3 o anche superiori, allora possono essere cancellati immediatamente, poiché svaniranno comunque quando alla fine ∆t tendere a zero. Dopo un po' di allenamento, vedrai immediatamente cosa deve essere lasciato e cosa deve essere immediatamente scartato. Esistono molte regole e formule per differenziare diversi tipi di funzioni. Puoi memorizzarli o utilizzare tabelle speciali. Un piccolo elenco di tali regole è riportato nella tabella. 8.3.

Passando alle applicazioni fisiche della derivata, utilizzeremo notazioni leggermente diverse da quelle accettate in fisica.

In primo luogo, la designazione delle funzioni cambia. In effetti, quali funzioni differenzieremo? Queste funzioni sono grandezze fisiche che dipendono dal tempo. Ad esempio, la coordinata di un corpo x(t) e la sua velocità v(t) possono essere date da formule come queste:

C'è un'altra notazione per la derivata, che è molto comune sia in matematica che in fisica:

(si legge ¾de x di de te¿).

Soffermiamoci più in dettaglio sul significato della notazione (29). Il matematico lo interpreta in due modi, o come limite:

o come frazione, il cui denominatore è l'incremento temporale dt, e il numeratore è il cosiddetto differenziale dx della funzione x(t). Il concetto di differenziale non è difficile, ma non lo discuteremo ora; ti sta aspettando nel primo piatto.

Il fisico, non vincolato dai requisiti del rigore matematico, comprende la notazione (29) in modo più informale. Sia dx la variazione di coordinata nel tempo dt. Prendiamo l'intervallo dt così piccolo che il rapporto dx=dt sia vicino al suo limite (30 ) con una precisione che ci soddisfa.

E poi, dirà il fisico, la derivata della coordinata rispetto al tempo è semplicemente una frazione, al numeratore della quale c'è una variazione sufficientemente piccola della coordinata dx, e al denominatore c'è un periodo di tempo sufficientemente piccolo dt, durante la quale si è verificata questa modifica della coordinata. Una comprensione così ampia della derivata è tipica del ragionamento in fisica. Inoltre, ci atterremo a questo livello fisico di rigore.

Torniamo all'esempio originale (26 ) e calcoliamo la derivata della coordinata, e allo stesso tempo osserviamo l'uso congiunto della notazione (28 ) e (29 ):

x(t) = 1 + 12t 3t2 ) x(t) =dt d (1 + 12t 3t2 ) = 12 6t:

(Il simbolo di derivazione dt d prima della parentesi è lo stesso del tratto sopra la parentesi nella vecchia notazione.)

Si noti che la derivata calcolata della coordinata è risultata uguale alla velocità del corpo (27). Non è un caso e dobbiamo discuterne in modo più dettagliato.

2.1 Coordinata derivata

Innanzitutto, notiamo che la velocità in (27 ) può essere sia positiva che negativa. Vale a dire, la velocità è positiva per t< 2, обращается в нуль при t = 2 и становится отрицательной при t > 2.

Cosa significa? È molto semplice: non si tratta del valore assoluto della velocità, ma della proiezione vx del vettore di velocità sull'asse X. Pertanto, al posto della (27), sarebbe più corretto scrivere:

Se hai dimenticato qual è la proiezione di un vettore su un asse, leggi la sezione corrispondente dell'articolo ¾ Vettori in fisica¿. Qui ricordiamo solo che il segno della proiezione vx riflette la relazione tra la direzione della velocità e la direzione dell'asse X:

vx > 0 , il corpo si muove nella direzione dell'asse X; vx< 0 , тело движется против оси X.

(Ad esempio, se vx = 3 m/s, significa che il corpo si sta muovendo a una velocità di 3 m/s nella direzione opposta all'asse X.)

Pertanto, nel nostro esempio (31 ) abbiamo il seguente quadro di moto: a t< 2 тело движется в положительном направлении оси X и постепенно замедляется; при t = 0 тело останавливается; при t >2 il corpo, accelerando, si muove nella direzione negativa dell'asse x.

Assumiamo che la velocità del corpo in valore assoluto sia uguale a v. Ci sono due casi di direzione del movimento.

1. Se il corpo si muove nella direzione positiva dell'asse X, allora una piccola variazione della coordinata dx è positiva e uguale alla traiettoria percorsa dal corpo nel tempo dt. Così

x = dx dt = v:

2. Se il corpo si muove nella direzione negativa dell'asse x, allora dx< 0. Путь за время dt равен dx, поэтому dx=dt = v или

x = dx dt = v:

Si noti ora che nel primo caso vx = v, e nel secondo caso vx = v. Pertanto, entrambi i casi sono combinati in un'unica formula:

e veniamo al fatto più importante: la derivata della coordinata del corpo è uguale alla proiezione della velocità del corpo sull'asse dato.

È facile vedere che il segno della funzione crescente (decrescente) funziona. Vale a dire:

x > 0) vx > 0) il corpo si muove nella direzione dell'asse X) la coordinata x aumenta; X< 0) vx < 0) тело двигается против оси X) координата x уменьшается:

2.2 Accelerazione

La velocità di un corpo caratterizza la velocità di variazione delle sue coordinate. Ma la velocità può anche cambiare più lentamente o più velocemente. Una caratteristica della velocità di variazione della velocità è una grandezza fisica chiamata accelerazione.

Sia, ad esempio, che la velocità di un'auto durante un'accelerazione uniforme aumenti da v0 = 2 m/s a v = 14 m/s nel tempo t = 3 s. L'accelerazione dell'auto si calcola con la formula:

Così, in un secondo, la velocità dell'auto aumenta di 4 m/s.

E qual è l'accelerazione se la velocità, al contrario, è diminuita da v0 = 14 m/s a v = 2 m/s nello stesso tempo t = 3 s? Quindi secondo la formula (33) otteniamo:

In un secondo, come si vede, la velocità diminuisce di 4 m/s.

Si può parlare di accelerazione se la velocità varia in modo non uniforme? Certo, è possibile, ma solo sarà un'accelerazione istantanea, che dipende anche dal tempo. Lo schema di ragionamento vi è già ben noto: nella formula (33) al posto dell'intervallo di tempo t prendiamo un piccolo intervallo dt, al posto della differenza v v0 prendiamo l'incremento dv della velocità nel tempo dt, e come un risultato otteniamo:

Pertanto, risulta che l'accelerazione è una derivata della velocità.

La formula (34 ), tuttavia, non descrive tutte le situazioni che si presentano in meccanica. Ad esempio, muovendosi uniformemente lungo una circonferenza, la velocità del corpo non cambia in valore assoluto, e secondo la (34) avremmo dovuto ottenere a = v = 0. Ma sai benissimo che il corpo ha accelerazione, è diretto verso il centro del cerchio ed è detto centripeto. Pertanto, la formula (34) necessita di alcune modifiche.

Questa modifica è collegata al fatto che l'accelerazione è in realtà un vettore. Si scopre che il vettore di accelerazione mostra la direzione del cambiamento nella velocità del corpo. Cosa significa, lo scopriremo ora con semplici esempi.

Lasciamo che il corpo si muova lungo l'asse X. Consideriamo due casi di direzione dell'accelerazione: rispettivamente lungo l'asse X e contro l'asse X.

1. Il vettore di accelerazione ~a è co-diretto con l'asse X (Fig. diciotto ). La proiezione dell'accelerazione sull'asse X è positiva: ax > 0.

Riso. 18. ascia > 0

V In questo caso, la velocità cambia nella direzione positiva dell'asse X. Vale a dire:

Se il corpo si sposta a destra (vx > 0), allora accelera: la velocità modulo del corpo aumenta. In questo caso, aumenta anche la proiezione della velocità vx.

Se il corpo si sposta a sinistra (vx< 0), то оно тормозит: скорость тела по модулю уменьшается. Но обратите внимание, что проекция скорости vx , будучи отрицательной, при этом увеличивается.

Pertanto, se ax > 0, la proiezione della velocità vx aumenta indipendentemente dal fatto che

in quale direzione si muove il corpo.

2. Il vettore di accelerazione ~a è diretto opposto all'asse X (Fig. diciannove). La proiezione dell'accelerazione sull'asse X è negativa: ax< 0.

Riso. 19.ax< 0

V In questo caso, la velocità cambia nella direzione negativa dell'asse X. Vale a dire:

Se il corpo si sposta a destra (vx > 0), allora rallenta: la velocità del modulo del corpo diminuisce. Anche in questo caso la proiezione della velocità vx diminuisce.

Se il corpo si sposta a sinistra (vx< 0), то оно разгоняется: скорость тела по модулю увеличивается. Но проекция скорости vx , будучи отрицательной, при этом уменьшается.

Quindi se ax< 0, то проекция скорости vx убывает, и опять-таки вне зависимости от того, в каком направлении движется тело.

La relazione tra il segno della proiezione di accelerazione ax e l'aumento (diminuzione) della proiezione di velocità vx trovato in questi esempi ci porta alla modifica desiderata della formula (34):

Esempio. Torniamo all'esempio (26):

x = 1 + 12t 3t2

(la coordinata è misurata in metri, il tempo in secondi). Differenziando due volte in successione, otteniamo:

vx=x=126t;

ax=vx=6:

Come puoi vedere, l'accelerazione è modulo costante e pari a 6 m/s2. Accelerazione diretta nella direzione opposta all'asse X.

L'esempio sopra è un caso di moto uniformemente accelerato, in cui il modulo e la direzione dell'accelerazione sono invariati (o, in breve, ~a = const). Il movimento uniformemente accelerato è uno dei tipi di movimento più importanti e frequenti in meccanica.

Da questo esempio, è facile capire che con un movimento uniformemente accelerato, la proiezione della velocità è una funzione lineare del tempo e la coordinata è una funzione quadratica.

Esempio. Considera un caso più esotico:

x = 2 + 3t 4t2 + 5t3 .

Il significato fisico della derivata. L'USO in matematica include un gruppo di compiti per la cui soluzione è necessaria la conoscenza e la comprensione del significato fisico della derivata. In particolare, ci sono compiti in cui è data la legge del moto di un certo punto (oggetto), espressa da un'equazione e si richiede di trovare la sua velocità in un determinato momento nel tempo del movimento, ovvero il tempo dopo il quale l'oggetto acquisisce una certa velocità data.I compiti sono molto semplici, si risolvono in un solo passaggio. Così:

Sia data la legge del moto di un punto materiale x (t) lungo l'asse delle coordinate, dove x è la coordinata del punto in movimento, t è il tempo.

La velocità in un dato momento è la derivata della coordinata rispetto al tempo. Questo è il significato meccanico della derivata.

Allo stesso modo, l'accelerazione è la derivata della velocità rispetto al tempo:

Pertanto, il significato fisico della derivata è velocità. Questa può essere la velocità di movimento, la velocità di un cambiamento in un processo (ad esempio, la crescita di batteri), la velocità di lavoro (e così via, ci sono molti compiti applicati).

Inoltre, è necessario conoscere la tabella delle derivate (è necessario conoscerla così come la tabella delle moltiplicazioni) e le regole di differenziazione. Nello specifico, per risolvere i problemi specificati, è necessario conoscere le prime sei derivate (vedi tabella):

Considera i compiti:

x (t) \u003d t 2 - 7t - 20

dove x t è il tempo in secondi misurato dall'inizio del movimento. Trova la sua velocità (in metri al secondo) al tempo t = 5 s.

Il significato fisico della derivata è velocità (velocità di movimento, velocità di cambiamento di processo, velocità di lavoro, ecc.)

Troviamo la legge della variazione di velocità: v (t) = x′(t) = 2t – 7 m/s.

Per t = 5 abbiamo:

Risposta: 3

Decidi da solo:

Il punto materiale si muove rettilineo secondo la legge x(t) = 6t 2 - 48t + 17, dove X- distanza dal punto di riferimento in metri, T- tempo in secondi, misurato dall'inizio del movimento. Trova la sua velocità (in metri al secondo) al tempo t = 9 s.

Il punto materiale si muove rettilineo secondo la legge x(t) = 0,5t 3 – 3t 2 + 2t, dove XT- tempo in secondi, misurato dall'inizio del movimento. Trova la sua velocità (in metri al secondo) al tempo t = 6 s.

Il punto materiale si muove in linea retta secondo la legge

x (t) = –t 4 + 6t 3 + 5t + 23

dove X- distanza dal punto di riferimento in metri,T- tempo in secondi, misurato dall'inizio del movimento. Trova la sua velocità (in metri al secondo) al tempo t = 3 s.

Il punto materiale si muove in linea retta secondo la legge

x (t) = (1/6) t 2 + 5 t + 28

dove x è la distanza in metri dal punto di riferimento, t è il tempo in secondi misurato dall'inizio del movimento. In quale momento (in secondi) la sua velocità era pari a 6 m/s?

Troviamo la legge del cambio di velocità:

Per sapere in che momentoTla velocità era pari a 3 m/s, occorre risolvere l'equazione:

Risposta: 3

Decidi tu stesso:

Un punto materiale si muove in linea retta secondo la legge x (t) \u003d t 2 - 13t + 23, dove X- distanza dal punto di riferimento in metri, T- tempo in secondi, misurato dall'inizio del movimento. In quale momento (in secondi) la sua velocità era pari a 3 m/s?

Il punto materiale si muove in linea retta secondo la legge

x (t) \u003d (1/3) t 3 - 3t 2 - 5t + 3

dove X- distanza dal punto di riferimento in metri, T- tempo in secondi, misurato dall'inizio del movimento. In quale momento (in secondi) la sua velocità era pari a 2 m/s?

Noto che non vale la pena concentrarsi solo su questo tipo di attività durante l'esame. Possono introdurre in modo del tutto inaspettato compiti inversi a quelli presentati. Quando viene data la legge del cambiamento della velocità, verrà sollevata la questione di trovare la legge del moto.

Suggerimento: in questo caso, è necessario trovare l'integrale della funzione velocità (anche queste sono attività in un'azione). Se è necessario trovare la distanza percorsa in un determinato momento, è necessario sostituire il tempo nell'equazione risultante e calcolare la distanza. Tuttavia, analizzeremo anche tali compiti, non perdetelo!Vi auguro il successo!

Cordiali saluti, Alexander Krutitskikh.

P.S: Ti sarei grato se parlassi del sito nei social network.

Finora abbiamo associato il concetto di derivata alla rappresentazione geometrica del grafico di una funzione. Sarebbe però un grave errore limitare il ruolo del concetto di derivata al solo problema di determinare la pendenza della tangente ad una data curva. Un compito ancora più importante da un punto di vista scientifico è il calcolo del tasso di variazione di qualsiasi quantità f(t), cambiando nel tempo t. Fu da questo lato che Newton si avvicinò al calcolo differenziale. In particolare, Newton cercò di analizzare il fenomeno della velocità, considerando come variabili il tempo e la posizione di una particella in movimento (secondo Newton, "fluenti"). Quando una certa particella si muove lungo l'asse x, il suo movimento è completamente determinato, poiché la funzione è data x = f(t), indicando la posizione della particella x in qualsiasi momento t. Il "movimento uniforme" con velocità b costante nell'asse x è determinato da una funzione lineare x = a + bt, dove a è la posizione della particella nel momento iniziale (per t = 0).

Il moto di una particella su un piano è già descritto da due funzioni

x = f(t), y = g(t),

che ne definiscono le coordinate in funzione del tempo. In particolare, due funzioni lineari corrispondono al moto uniforme

x = a + bt, y = c + dt,

dove b e d sono le due "componenti" della velocità costante, e a e c sono le coordinate della posizione iniziale della particella (a t = 0); la traiettoria della particella è una linea retta, la cui equazione è

(x - a) d - (y - c) b = 0

si ottiene eliminando t dalle due relazioni precedenti.

Se una particella si muove nel piano verticale x, y sotto l'azione della sola gravità, allora il suo moto (questo è dimostrato in fisica elementare) è determinato da due equazioni

dove a, b, c, d sono costanti dipendenti dallo stato della particella nel momento iniziale e g è l'accelerazione di gravità, che è circa 9,81 se si misura il tempo in secondi e la distanza in metri. La traiettoria di moto ottenuta eliminando t da queste due equazioni è una parabola

Se solo b≠0; in caso contrario, la traiettoria è un segmento dell'asse verticale.

Se la particella è costretta a muoversi lungo una determinata curva (proprio come un treno si muove lungo i binari), allora il suo movimento può essere determinato dalla funzione s (t) (una funzione del tempo t) uguale alla lunghezza dell'arco s calcolata lungo la curva data da un punto di partenza Р 0 alla posizione della particella nel punto P al tempo t. Ad esempio, se stiamo parlando di un cerchio unitario x 2 + y 2 = 1, quindi la funzione s = ct determina su questo cerchio un moto rotatorio uniforme con una velocità Con.

* L'esercizio. Disegna le traiettorie dei moti piani dati dalle equazioni: 1) x \u003d sin t, y \u003d costo t; 2) x = sin 2t, y = cos 3t; 3) x \u003d peccato 2t, y \u003d 2 peccato 3t; 4) nel moto parabolico sopra descritto, assumere la posizione iniziale della particella (a t = 0) all'origine e assumere b>0, d>0. Trova le coordinate del punto più alto della traiettoria. Trova il tempo t e il valore x corrispondente alla seconda intersezione della traiettoria con l'asse x.

Il primo obiettivo di Newton era trovare la velocità di una particella che si muove in modo non uniforme. Consideriamo, per semplicità, il moto di una particella lungo una retta data dalla funzione x = f(t). Se il moto fosse uniforme, cioè effettuato a velocità costante, allora questa velocità potrebbe essere trovata prendendo due istanti di tempo t e t 1 e le posizioni corrispondenti delle particelle f(t) e f(t1) e fare una relazione

Ad esempio, se t è misurato in ore e x è in chilometri, allora t 1 - t \u003d 1 differenza x 1 - x sarà il numero di chilometri percorsi in 1 ora, e v- velocità (in chilometri orari). Dicendo che la velocità è un valore costante, intendono solo che il rapporto di differenza

non cambia per nessun valore di t e t 1 . Ma se il moto è irregolare (come avviene, ad esempio, quando un corpo è in caduta libera, la cui velocità aumenta con la caduta), allora la relazione (3) non dà il valore della velocità al momento t , ma rappresenta quella che comunemente viene chiamata la velocità media nell'intervallo di tempo da t a t 1 . Per prendere velocità al tempo t, devi calcolare il limite velocità media poiché t 1 tende a t. Quindi, seguendo Newton, definiamo la velocità come segue:

In altre parole, la velocità è la derivata della distanza percorsa (le coordinate della particella sulla retta) rispetto al tempo, o il "velocità di variazione istantanea" del percorso rispetto al tempo - al contrario di mezzo il tasso di variazione determinato dalla formula (3).

La velocità di variazione della velocità stessa chiamato accelerazione. L'accelerazione è solo una derivata di una derivata; è solitamente indicato dal simbolo f "(t) ed è chiamato derivata seconda dalla funzione f(t).