Το βίντεο φροντιστήριο «Κατασκευή με πυξίδα και χάρακα» περιέχει εκπαιδευτικό υλικό, το οποίο αποτελεί τη βάση για την επίλυση κατασκευαστικών προβλημάτων. Οι γεωμετρικές κατασκευές αποτελούν σημαντικό μέρος της επίλυσης πολλών πρακτικών εργασιών. Σχεδόν καμία γεωμετρική εργασία δεν μπορεί να κάνει χωρίς τη δυνατότητα να αντικατοπτρίζει σωστά τις συνθήκες στο σχήμα. Ο κύριος στόχος αυτού του μαθήματος βίντεο είναι να εμβαθύνει τις γνώσεις του μαθητή σχετικά με τη χρήση εργαλείων σχεδίασης για την κατασκευή γεωμετρικών σχημάτων, να επιδείξει τις δυνατότητες αυτών των εργαλείων και να διδάξει πώς να λύνει απλές εργασίες κατασκευής.

Η μάθηση με τη βοήθεια ενός μαθήματος βίντεο έχει πολλά πλεονεκτήματα, συμπεριλαμβανομένης της σαφήνειας, της σαφήνειας των κατασκευών που παράγονται, καθώς το υλικό αποδεικνύεται με ηλεκτρονικά μέσα κοντά στην πραγματική κατασκευή στον πίνακα. Οι κατασκευές είναι ευδιάκριτες από οποιοδήποτε σημείο της τάξης, σημαντικά σημεία επισημαίνονται με χρώμα. Και η φωνητική συνοδεία αντικαθιστά την παρουσίαση ενός τυπικού μπλοκ εκπαιδευτικού υλικού από τον δάσκαλο.

Το εκπαιδευτικό βίντεο ξεκινά με την ανακοίνωση του ονόματος του θέματος. Υπενθυμίζεται στους μαθητές ότι έχουν ήδη κάποιες δεξιότητες στην κατασκευή γεωμετρικών σχημάτων. Στα προηγούμενα μαθήματα, όταν οι μαθητές μελετούσαν τις βασικές αρχές της γεωμετρίας και κατέκτησαν τις έννοιες της ευθείας γραμμής, ενός σημείου, μιας γωνίας, ενός τμήματος, ενός τριγώνου, σχεδίαζαν τμήματα ίσα με τα δεδομένα, ολοκλήρωσαν την κατασκευή των απλούστερων γεωμετρικών σχημάτων. Τέτοιες κατασκευές δεν απαιτούν πολύπλοκες δεξιότητες, αλλά η σωστή εκτέλεση των εργασιών είναι σημαντική για την περαιτέρω εργασία με γεωμετρικά αντικείμενα και την επίλυση πιο περίπλοκων γεωμετρικών προβλημάτων.

Δίνεται στους μαθητές μια λίστα με τα κύρια εργαλεία που χρησιμοποιούνται για την εκτέλεση κατασκευών κατά την επίλυση γεωμετρικών προβλημάτων. Οι εικόνες δείχνουν έναν χάρακα κλίμακας, μια πυξίδα, ένα τρίγωνο με ορθή γωνία, ένα μοιρογνωμόνιο.

Διευρύνοντας την κατανόηση των μαθητών σχετικά με τον τρόπο εκτέλεσης διαφορετικών τύπων κατασκευών, τους συνιστάται να δώσουν προσοχή σε κατασκευές που εκτελούνται χωρίς χάρακα κλίμακας και για αυτούς μπορούν να χρησιμοποιηθούν μόνο πυξίδες και χάρακα χωρίς διαιρέσεις. Σημειώνεται ότι μια τέτοια ομάδα κατασκευαστικών εργασιών, στις οποίες χρησιμοποιείται μόνο χάρακας και πυξίδα, ξεχωρίζεται χωριστά στη γεωμετρία.

Προκειμένου να προσδιοριστούν ποια γεωμετρικά προβλήματα μπορούν να λυθούν χρησιμοποιώντας έναν χάρακα και μια πυξίδα, προτείνεται να εξεταστούν οι δυνατότητες αυτών των εργαλείων σχεδίασης. Ο χάρακας βοηθά να χαράξουμε μια αυθαίρετη γραμμή, να χτίσουμε μια γραμμή που διέρχεται από ορισμένα σημεία. Η πυξίδα έχει σχεδιαστεί για να σχεδιάζει κύκλους. Μόνο με τη βοήθεια μιας πυξίδας κατασκευάζεται ένας αυθαίρετος κύκλος. Με τη βοήθεια μιας πυξίδας σχεδιάζεται επίσης ένα τμήμα ίσο με αυτό. Οι υποδεικνυόμενες δυνατότητες των εργαλείων σχεδίασης καθιστούν δυνατή την εκτέλεση ορισμένων εργασιών κατασκευής. Μεταξύ τέτοιων εργασιών κατασκευής:

1. κατασκευή γωνίας ίσης με δεδομένη.
2. σχεδιάζοντας μια γραμμή κάθετη στη δεδομένη, που διέρχεται από το καθορισμένο σημείο.
3. διαίρεση ενός τμήματος σε δύο ίσα μέρη.
4. μια σειρά άλλων κατασκευαστικών εργασιών.

Στη συνέχεια, προτείνεται η επίλυση του έργου κατασκευής με χρήση χάρακα και πυξίδας. Η οθόνη δείχνει την κατάσταση του προβλήματος, η οποία συνίσταται στην τοποθέτηση ενός τμήματος σε μια συγκεκριμένη ακτίνα ίσο με ένα συγκεκριμένο τμήμα από την αρχή της ακτίνας. Η λύση αυτού του προβλήματος ξεκινά με την κατασκευή ενός αυθαίρετου τμήματος ΑΒ και ενός συστήματος ακτίνων. Ως λύση σε αυτό το πρόβλημα, προτείνεται η κατασκευή ενός κύκλου με ακτίνα ΑΒ και κέντρο στο σημείο Ο. Μετά την κατασκευή, ο κατασκευασμένος κύκλος τέμνεται με την ακτίνα OS σε κάποιο σημείο D. Στην περίπτωση αυτή, το τμήμα της ακτίνας που αντιπροσωπεύεται από το τμήμα OD είναι το τμήμα ίσο με το τμήμα ΑΒ. Το πρόβλημα λύθηκε.

Το βίντεο μάθημα «Κατασκευή με πυξίδα και χάρακα» μπορεί να χρησιμοποιηθεί όταν ο δάσκαλος εξηγεί τα βασικά για την επίλυση πρακτικών προβλημάτων για την κατασκευή. Επίσης, αυτή η μέθοδος μπορεί να κατακτηθεί με ανεξάρτητη μελέτη αυτού του υλικού. Αυτό το βίντεο μάθημα μπορεί επίσης να βοηθήσει τον δάσκαλο με την εξ αποστάσεως υποβολή υλικού για αυτό το θέμα.

Εγκυκλοπαιδικό YouTube

1 / 5

✪ 7η τάξη, μάθημα 22, Κατασκευές με πυξίδα και χάρακα

✪ Geometry 7 Circle Constructions με πυξίδα και χάρακα

✪ Κατασκευή τριγώνου σε δύο πλευρές και γωνία μεταξύ τους

✪ Γεωμετρία 7 Παραδείγματα προβλημάτων κατασκευής

✪ Βαθμός 7, Μάθημα 23, Παραδείγματα εργασιών κατασκευής

Υπότιτλοι

Παραδείγματα

Πρόβλημα διχοτόμησης. Χρησιμοποιήστε μια πυξίδα και μια ευθεία για να διαιρέσετε αυτό το τμήμα ΑΒσε δύο ίσα μέρη. Μία από τις λύσεις φαίνεται στο σχήμα:

• Οι πυξίδες σχεδιάζουν κύκλους με κέντρο σε σημεία ΕΝΑκαι σιακτίνα κύκλου ΑΒ.
• Εύρεση σημείων τομής Πκαι Qδύο κατασκευασμένοι κύκλοι (τόξα).
• Σε έναν χάρακα, σχεδιάστε ένα τμήμα ή μια γραμμή που διέρχεται από τα σημεία Πκαι Q.
• Εύρεση του μέσου του τμήματος ΑΒ- σημείο τομής ΑΒκαι PQ.

Επίσημος ορισμός

Στα κατασκευαστικά προβλήματα, εξετάζεται ένα σύνολο από τα ακόλουθα αντικείμενα: όλα τα σημεία του επιπέδου, όλες οι γραμμές του επιπέδου και όλοι οι κύκλοι του επιπέδου. Στις συνθήκες του προβλήματος, αρχικά προσδιορίζεται ένα συγκεκριμένο σύνολο αντικειμένων (θεωρείται κατασκευασμένο). Επιτρέπεται η προσθήκη (δόμηση) στο σύνολο των κτισμένων αντικειμένων:

1. αυθαίρετο σημείο?
2. ένα αυθαίρετο σημείο σε μια δεδομένη γραμμή.
3. ένα αυθαίρετο σημείο σε έναν δεδομένο κύκλο.
4. το σημείο τομής δύο δεδομένων ευθειών.
5. σημεία τομής/εφαπτομένης μιας δεδομένης ευθείας γραμμής και ενός δεδομένου κύκλου.
6. σημεία τομής/εφαπτομένης δύο δεδομένων κύκλων.
7. μια αυθαίρετη γραμμή που διέρχεται από ένα δεδομένο σημείο.
8. μια ευθεία γραμμή που διέρχεται από δύο δεδομένα σημεία.
9. ένας αυθαίρετος κύκλος με κέντρο σε ένα δεδομένο σημείο.
10. ένας αυθαίρετος κύκλος με ακτίνα ίση με την απόσταση μεταξύ δύο δεδομένων σημείων.
11. κύκλος με κέντρο σε ένα δεδομένο σημείο και με ακτίνα ίση με την απόσταση μεταξύ δύο δεδομένων σημείων.

Απαιτείται, με τη βοήθεια ενός πεπερασμένου αριθμού αυτών των πράξεων, να κατασκευαστεί ένα άλλο σύνολο αντικειμένων που βρίσκεται σε μια δεδομένη σχέση με το αρχικό σύνολο.

Η λύση του κατασκευαστικού προβλήματος περιλαμβάνει τρία βασικά μέρη:

1. Περιγραφή της μεθόδου για την κατασκευή ενός δεδομένου συνόλου.
2. Μια απόδειξη ότι το σύνολο που κατασκευάστηκε με τον τρόπο που περιγράφηκε είναι πράγματι σε μια δεδομένη σχέση με το αρχικό σύνολο. Συνήθως η απόδειξη της κατασκευής γίνεται ως κανονική απόδειξη ενός θεωρήματος, στηριζόμενος σε αξιώματα και άλλα αποδεδειγμένα θεωρήματα.
3. Ανάλυση της περιγραφόμενης μεθόδου κατασκευής για τη δυνατότητα εφαρμογής της σε διαφορετικές παραλλαγές αρχικών συνθηκών, καθώς και για τη μοναδικότητα ή τη μη μοναδικότητα της λύσης που λαμβάνεται με την περιγραφόμενη μέθοδο.

Γνωστά προβλήματα

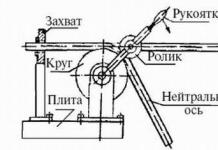
Ένα άλλο γνωστό και άλυτο έργο με τη βοήθεια πυξίδας και χάρακα είναι η κατασκευή ενός τριγώνου σύμφωνα με τρία δεδομένα μήκη διχοτόμων. Αυτό το πρόβλημα παραμένει άλυτο ακόμη και με την παρουσία ενός εργαλείου που εκτελεί την τριτομή μιας γωνίας, όπως ένα tomahawk.

Επιτρεπόμενα τμήματα για κατασκευή με χρήση πυξίδας και χάρακα

Χρησιμοποιώντας αυτά τα εργαλεία, είναι δυνατό να κατασκευαστεί ένα τμήμα, το οποίο σε μήκος:

Για να κατασκευαστεί ένα τμήμα με μήκος αριθμητικά ίσο με το γινόμενο, την ιδιωτική και την τετραγωνική ρίζα των μηκών των δεδομένων τμημάτων, είναι απαραίτητο να ορίσετε ένα τμήμα μονάδας στο επίπεδο κατασκευής (δηλαδή ένα τμήμα μήκους 1). Η εξαγωγή ριζών από τμήματα με άλλες φυσικές δυνάμεις που δεν είναι δύναμη 2 δεν είναι δυνατή με χρήση πυξίδας και ευθυγράμμισης. Έτσι, για παράδειγμα, είναι αδύνατο να κατασκευαστεί ένα τμήμα μήκους από ένα μόνο τμήμα χρησιμοποιώντας μια πυξίδα και έναν χάρακα. Αυτό το γεγονός, ειδικότερα, συνεπάγεται τη μη επίλυση του προβλήματος του διπλασιασμού του κύβου.

Πιθανές και αδύνατες κατασκευές

Από τυπική άποψη, η λύση οποιουδήποτε κατασκευαστικού προβλήματος ανάγεται σε μια γραφική λύση κάποιας αλγεβρικής εξίσωσης και οι συντελεστές αυτής της εξίσωσης σχετίζονται με τα μήκη των δεδομένων τμημάτων. Επομένως, μπορούμε να πούμε ότι το πρόβλημα της κατασκευής περιορίζεται στην εύρεση των πραγματικών ριζών κάποιας αλγεβρικής εξίσωσης.

Επομένως, είναι βολικό να μιλάμε για την κατασκευή ενός αριθμού - μια γραφική λύση σε μια εξίσωση ενός συγκεκριμένου τύπου.

Με βάση τις πιθανές κατασκευές τμημάτων, είναι δυνατές οι ακόλουθες κατασκευές:

• Κατασκευή λύσεων γραμμικών εξισώσεων.
• Κατασκευή λύσεων σε εξισώσεις που ανάγονται σε λύσεις δευτεροβάθμιων εξισώσεων.

Με άλλα λόγια, είναι δυνατό να κατασκευαστούν μόνο τμήματα ίσα με αριθμητικές παραστάσεις χρησιμοποιώντας την τετραγωνική ρίζα των αρχικών αριθμών (δεδομένα μήκη τμημάτων).

Είναι σημαντικό να σημειωθεί ότι είναι σημαντικό η λύση να εκφράζεται χρησιμοποιώντας τετράγωνορίζες, όχι ριζοσπάστες αυθαίρετου βαθμού. Ακόμα κι αν μια αλγεβρική εξίσωση έχει λύση σε ρίζες, τότε δεν προκύπτει από αυτό ότι μια πυξίδα και ένας χάρακας μπορούν να κατασκευάσουν ένα τμήμα ίσο με τη λύση του. Η απλούστερη εξίσωση είναι: x 3 − 2 = 0 , (\displaystyle x^(3)-2=0,)σχετίζεται με το περίφημο πρόβλημα του διπλασιασμού του κύβου, το οποίο ανάγεται σε αυτή την κυβική εξίσωση. Όπως αναφέρθηκε παραπάνω, η λύση αυτής της εξίσωσης ( 2 3 (\displaystyle (\sqrt[(3)](2)))) δεν μπορεί να κατασκευαστεί με πυξίδα και ευθεία.

Η ικανότητα κατασκευής ενός κανονικού 17-gon προκύπτει από την έκφραση για το συνημίτονο της κεντρικής γωνίας της πλευράς του:

cos ⁡ (2 π 17) = − 1 16 + 1 16 17 + 1 16 34 − 2 17 + (\displaystyle \cos (\left((\frac (2\pi )(17))\right))=- (\frac (1)(16))\;+\;(\frac (1)(16))(\sqrt (17))\;+\;(\frac (1)(16))(\sqrt (34-2(\sqrt (17))))\;+\;) + 1 8 17 + 3 17 − 34 − 2 17 − 2 34 + 2 17 , (\displaystyle +(\frac (1)(8))(\sqrt (17+3(\sqrt (17))-(\ sqrt (34-2(\sqrt (17))))-2(\sqrt (34+2(\sqrt (17))))))που με τη σειρά του προκύπτει από τη δυνατότητα αναγωγής μιας εξίσωσης της μορφής x F n − 1 = 0 , (\displaystyle x^(F_(n))-1=0,)που F n (\displaystyle F_(n))- οποιοσδήποτε πρώτος αριθμός Fermat , αλλάζοντας τη μεταβλητή σε τετραγωνική εξίσωση.

Παραλλαγές και γενικεύσεις

• Κατασκευές με ενιαία πυξίδα.Σύμφωνα με το θεώρημα Mohr-Mascheroni, με τη βοήθεια μιας πυξίδας, μπορείτε να κατασκευάσετε οποιοδήποτε σχήμα που μπορεί να κατασκευαστεί με πυξίδα και χάρακα. Στην περίπτωση αυτή, μια ευθεία θεωρείται ότι έχει κατασκευαστεί εάν δίνονται δύο σημεία πάνω της.
• Κατασκευές με έναν μόνο χάρακα.Είναι προφανές ότι μόνο προβολικά αμετάβλητες κατασκευές μπορούν να πραγματοποιηθούν με τη βοήθεια ενός χάρακα. Συγκεκριμένα,
  • είναι αδύνατο ακόμη και να χωριστεί το τμήμα σε δύο ίσα μέρη,
  • είναι επίσης αδύνατο να βρεθεί το κέντρο του δεδομένου κύκλου.

Αλλά,

• εάν υπάρχει ένας προσχεδιασμένος κύκλος στο επίπεδο με ένα σημειωμένο κέντρο με έναν χάρακα, μπορείτε να εκτελέσετε τις ίδιες κατασκευές όπως με μια πυξίδα και έναν χάρακα (

Το υλικό αυτής της παραγράφου μπορεί να χρησιμοποιηθεί σε εξωσχολικές δραστηριότητες. Μπορεί να παρουσιαστεί στους φοιτητές τόσο με τη μορφή διάλεξης όσο και με τη μορφή φοιτητικών εκθέσεων.

Για πολλούς αιώνες, πολλή προσοχή έχει τραβηχτεί σε προβλήματα που ήταν από καιρό γνωστά ως «διάσημα προβλήματα της αρχαιότητας». Τρία διάσημα προβλήματα εμφανίζονταν συνήθως με αυτό το όνομα:

1) τετραγωνίζοντας τον κύκλο,

2) τριτομή γωνίας,

3) διπλασιασμός του κύβου.

Όλα αυτά τα καθήκοντα προέκυψαν στην αρχαιότητα από τις πρακτικές ανάγκες των ανθρώπων. Στο πρώτο στάδιο της ύπαρξής τους, λειτουργούσαν ως υπολογιστικές εργασίες: σύμφωνα με ορισμένες «συνταγές», υπολογίστηκαν κατά προσέγγιση τιμές των απαιτούμενων ποσοτήτων (εμβαδόν κύκλου, περιφέρεια κ.λπ.). Στο δεύτερο στάδιο της ιστορίας αυτών των προβλημάτων, λαμβάνουν χώρα σημαντικές αλλαγές στη φύση τους: γίνονται γεωμετρικά (κατασκευαστικά) προβλήματα.

Στην αρχαία Ελλάδα, κατά την περίοδο αυτή, τους δόθηκαν κλασικές διατυπώσεις:

1) Κατασκευάστε ένα τετράγωνο που είναι ίσο σε μέγεθος με έναν δεδομένο κύκλο.

2) διαιρέστε τη δεδομένη γωνία σε τρία ίσα μέρη.

3) Κατασκευάστε μια άκρη ενός νέου κύβου, ο όγκος του οποίου θα ήταν διπλάσιος από τον δεδομένο κύβο.

Όλες αυτές οι γεωμετρικές κατασκευές προτάθηκαν να πραγματοποιηθούν με τη βοήθεια πυξίδας και χάρακα.

Η απλότητα της διατύπωσης αυτών των εργασιών και οι «ανυπέρβλητες δυσκολίες» που συναντήθηκαν στον δρόμο προς την επίλυσή τους συνέβαλαν στην αύξηση της δημοτικότητάς τους. Σε μια προσπάθεια να δώσουν αυστηρές λύσεις σε αυτά τα προβλήματα, οι αρχαίοι Έλληνες επιστήμονες έλαβαν πολλά σημαντικά αποτελέσματα για τα μαθηματικά, τα οποία συνέβαλαν στη μετατροπή της ετερόκλητης μαθηματικής γνώσης σε μια ανεξάρτητη παραγωγική επιστήμη (οι Πυθαγόρειοι, ο Ιπποκράτης της Χίου και ο Αρχιμήδης άφησαν μια ιδιαίτερα αξιοσημείωτο σημάδι εκείνη την εποχή).

Το πρόβλημα του διπλασιασμού του κύβου.

Η εργασία του διπλασιασμού ενός κύβου είναι η εξής: γνωρίζοντας την άκρη ενός δεδομένου κύβου, κατασκευάστε μια άκρη ενός τέτοιου κύβου, ο όγκος του οποίου θα ήταν διπλάσιος από τον όγκο του δεδομένου κύβου.

Έστω a το μήκος της άκρης του δεδομένου κύβου, x το μήκος της άκρης του επιθυμητού κύβου. Έστω - ο όγκος αυτού του κύβου και - ο όγκος του επιθυμητού κύβου, τότε σύμφωνα με τον τύπο για τον υπολογισμό του όγκου του κύβου έχουμε ότι: =, και εφόσον, σύμφωνα με την κατάσταση του προβλήματος, φτάνουμε στο εξίσωση.

Είναι γνωστό από την άλγεβρα ότι οι ορθολογικές ρίζες της ανηγμένης εξίσωσης με ακέραιους συντελεστές μπορούν να είναι μόνο ακέραιοι και να περιέχονται μεταξύ των διαιρετών του ελεύθερου όρου της εξίσωσης. Όμως οι διαιρέτες του αριθμού 2 είναι μόνο οι αριθμοί +1, -1, +2, -2 και κανένας από αυτούς δεν ικανοποιεί την αρχική εξίσωση. Επομένως, η εξίσωση δεν έχει ορθολογικές ρίζες, πράγμα που σημαίνει ότι το πρόβλημα του διπλασιασμού του κύβου δεν μπορεί να λυθεί χρησιμοποιώντας πυξίδα και ευθεία.

Το πρόβλημα του διπλασιασμού ενός κύβου με πυξίδα και ευθεία μπορεί να λυθεί μόνο κατά προσέγγιση. Ας παρουσιάσουμε μια από τις απλούστερες μεθόδους για μια κατά προσέγγιση λύση αυτού του προβλήματος.

Έστω AB=BC=a, και ABBC. Κατασκευάζουμε AD=AC και μετά CD με ακρίβεια 1%. Πράγματι, CD 1.2586…. Ταυτόχρονα =1,2599….

Το πρόβλημα του τετραγωνισμού ενός κύκλου.

Αιτιολόγηση της μη επιλύσεως του προβλήματος με χρήση πυξίδας και ευθείας.

Η εργασία του τετραγωνισμού ενός κύκλου είναι η εξής: να κατασκευαστεί ένα τετράγωνο ίσου εμβαδού με έναν κύκλο.

Έστω - η ακτίνα του δεδομένου κύκλου, - το μήκος της πλευράς του επιθυμητού τετραγώνου. Μετά, από εδώ.

Επομένως, το πρόβλημα του τετραγωνισμού ενός κύκλου θα λυθεί αν κατασκευάσουμε ένα τμήμα με μήκος. Εάν η ακτίνα αυτού του κύκλου ληφθεί ως μοναδιαίο τμήμα (= 1), τότε η ύλη θα μειωθεί στην κατασκευή ενός τμήματος μήκους κατά μήκος ενός τμήματος μονάδας.

Όπως γνωρίζετε, γνωρίζοντας το μοναδιαίο τμήμα, μπορούμε να κατασκευάσουμε μόνο τέτοια τμήματα με πυξίδα και χάρακα, τα μήκη των οποίων εκφράζονται σε ορθολογικούς αριθμούς χρησιμοποιώντας ένα πεπερασμένο σύνολο ορθολογικών πράξεων και εξάγοντας τετραγωνικές ρίζες και, επομένως, είναι αλγεβρικά αριθμοί. Σε αυτήν την περίπτωση, δεν θα χρησιμοποιηθούν όλοι οι αλγεβρικοί αριθμοί. Για παράδειγμα, δεν μπορείτε να κατασκευάσετε ένα τμήμα με μήκος κ.λπ.

Το 1882, ο Lindemann απέδειξε ότι είναι υπερβατικό. Από αυτό προκύπτει ότι είναι αδύνατο να κατασκευαστεί ένα τμήμα μήκους με πυξίδα και χάρακα και, επομένως, το πρόβλημα του τετραγωνισμού ενός κύκλου είναι άλυτο με αυτά τα μέσα.

Κατά προσέγγιση λύση του προβλήματος με χρήση πυξίδας και ευθυγράμμισης.

Εξετάστε μια από τις μεθόδους κατά προσέγγιση κατασκευής τμημάτων μήκους. Αυτή η προσέγγιση είναι η εξής. Ένα τέταρτο του κύκλου ΑΒ με κέντρο στο σημείο Ο και ακτίνα ίση με ένα διαιρείται στο μισό με το σημείο C. Στη συνέχεια της διαμέτρου CD, αφήστε στην άκρη το τμήμα ΔΕ ίσο με την ακτίνα. Από το σημείο Ε, σχεδιάζουμε τις ακτίνες ΕΑ και ΕΒ στην τομή με την εφαπτομένη στο σημείο Γ. Το τμήμα αποκοπής ΑΒ είναι περίπου ίσο με το μήκος του τόξου ΑΒ και το διπλασιασμένο είναι το ημικύκλιο.

Το σχετικό σφάλμα αυτής της προσέγγισης δεν υπερβαίνει το 0,227%.

Πρόβλημα τριτομής γωνίας.

Αιτιολόγηση της μη επιλύσεως του προβλήματος με χρήση πυξίδας και ευθείας.

Το πρόβλημα της τριτοτομής γωνίας είναι το εξής.: χωρίστε τη δεδομένη γωνία σε τρία ίσα μέρη.

Περιοριζόμαστε στην επίλυση του προβλήματος για γωνίες που δεν υπερβαίνουν το 90. Αν είναι αμβλεία γωνία, τότε =180-, όπου<90, так что, и поэтому задача о трисекции тупого угла сводится к задаче о трисекции острого угла.

Σημειώστε ότι (παρουσία ενός μόνο τμήματος) το πρόβλημα της κατασκευής της γωνίας (90) είναι ισοδύναμο με το πρόβλημα της κατασκευής του τμήματος x=cos. Αν μάλιστα η γωνία είναι κατασκευασμένη, τότε η κατασκευή του τμήματος x=cos ανάγεται στην κατασκευή ενός ορθογώνιου τριγώνου κατά μήκος της υποτείνουσας και της οξείας γωνίας.

Πίσω. Εάν κατασκευαστεί ένα τμήμα x, τότε η κατασκευή μιας τέτοιας γωνίας που x \u003d cos μειώνεται στην κατασκευή ενός ορθογωνίου τριγώνου κατά μήκος της υποτείνουσας και του σκέλους.

Έστω η δεδομένη γωνία, η επιθυμητή γωνία, άρα =. Τότε cos=cos 3. Είναι γνωστό ότι cos 3= 4cos-3cos . Επομένως, υποθέτοντας cos = και cos =, καταλήγουμε στην εξίσωση:

cos=4cos-3cos,

Ένα τμήμα, άρα και μια γωνία, μπορεί να κατασκευαστεί μόνο εάν αυτή η εξίσωση έχει τουλάχιστον μία ορθολογική ρίζα. Αλλά αυτό δεν ισχύει για όλους, και επομένως το πρόβλημα της τριτοτομής μιας γωνίας, μιλώντας γενικά, δεν μπορεί να λυθεί με τη βοήθεια μιας πυξίδας και μιας ευθυγράμμισης. Για παράδειγμα. Στο =60 παίρνουμε =1 και η εξίσωση που βρέθηκε παίρνει τη μορφή: . Είναι εύκολο να επαληθευτεί ότι αυτή η εξίσωση δεν έχει καμία ορθολογική ρίζα, πράγμα που συνεπάγεται την αδυναμία διαίρεσης μιας γωνίας 60 σε τρία ίσα μέρη χρησιμοποιώντας πυξίδα και ευθεία. Έτσι, το πρόβλημα της τριτομής μιας γωνίας δεν είναι επιλύσιμο από μια πυξίδα και μια ευθεία σε γενικές γραμμές.

Κατά προσέγγιση λύση του προβλήματος με χρήση πυξίδας και ευθυγράμμισης.

Εξετάστε έναν από τους τρόπους προσέγγισης της λύσης του προβλήματος χρησιμοποιώντας πυξίδα και χάρακα, που πρότεινε ο Albert Dürer (1471-1528).

Ας δοθεί γωνία ASB. Από την κορυφή S, περιγράφουμε έναν κύκλο με αυθαίρετη ακτίνα και συνδέουμε τα σημεία τομής των πλευρών της γωνίας με τον κύκλο με τη χορδή ΑΒ. Διαιρούμε αυτή τη χορδή σε τρία ίσα μέρη στα σημεία R και R (A R \u003d R R \u003d RВ). από τα σημεία Α και Β, όπως από κέντρα, με ακτίνες A R \u003d RВ περιγράφουμε τόξα που τέμνουν τον κύκλο στα σημεία T και T. Ας πραγματοποιήσουμε RSAB. Με ακτίνες A S \u003d BS, σχεδιάζουμε τόξα που τέμνουν το AB στα σημεία U και U. Τα τόξα AT, SS και TB είναι ίσα μεταξύ τους, αφού συστέλλονται από ίσες χορδές.

Για να βρει τα σημεία τριτοτομής της γωνίας X και X, ο Dürer διαιρεί τα τμήματα RU και RU σε τρία ίσα μέρη με τα σημεία PV και PV. Στη συνέχεια, με ακτίνες AV και BV, σχεδιάζουμε τόξα που τέμνουν τον κύκλο στα σημεία X και X. Συνδέοντας αυτά τα σημεία με το S, έχουμε τη διαίρεση αυτής της γωνίας σε τρία ίσα μέρη με καλή προσέγγιση στις πραγματικές τιμές.

Εισαγωγή.

II. Κύριο μέρος:

Κατασκευή τμήματος ίσου με το γινόμενο των άλλων δύο με χρήση πυξίδας και χάρακα:

1. η πρώτη μέθοδος κατασκευής?

   η δεύτερη μέθοδος κατασκευής?

   ο τρίτος τρόπος κατασκευής,

δ) η τέταρτη μέθοδος κατασκευής.

2) Κατασκευή τμήματος ίσου με την αναλογία των άλλων δύο με χρήση πυξίδας και χάρακα:

η πρώτη μέθοδος κατασκευής?

δεύτερη μέθοδος κατασκευής.

Συμπέρασμα.

Παράρτημα.

Εισαγωγή

Οι γεωμετρικές κατασκευές, ή η θεωρία των γεωμετρικών κατασκευών, είναι ένας κλάδος της γεωμετρίας όπου μελετώνται ερωτήσεις και μέθοδοι κατασκευής γεωμετρικών σχημάτων χρησιμοποιώντας ορισμένα κατασκευαστικά στοιχεία. Οι γεωμετρικές κατασκευές μελετώνται τόσο στη γεωμετρία του Ευκλείδη όσο και σε άλλες γεωμετρίες, τόσο στο επίπεδο όσο και στο διάστημα. Τα κλασικά εργαλεία κατασκευής είναι πυξίδες και χάρακας (μονόπλευρος μαθηματικός), ωστόσο, υπάρχουν κατασκευές με άλλα εργαλεία: μόνο μία πυξίδα, μόνο ένας χάρακας, εάν ένας κύκλος και το κέντρο του είναι σχεδιασμένα στο επίπεδο, μόνο ένας χάρακας με παράλληλο άκρες κλπ.

Όλα τα κατασκευαστικά προβλήματα βασίζονται σε δομικά αξιώματα, δηλαδή στα απλούστερα στοιχειώδη κατασκευαστικά προβλήματα, και ένα πρόβλημα θεωρείται λυμένο εάν αναχθεί σε έναν πεπερασμένο αριθμό από αυτά τα απλούστερα θετικά προβλήματα.

Φυσικά, κάθε όργανο έχει τη δική του εποικοδομητική δύναμη - το δικό του σύνολο αξιωμάτων. Έτσι, είναι γνωστό ότι είναι αδύνατο να διαιρέσετε ένα τμήμα χρησιμοποιώντας μόνο έναν χάρακα σε δύο ίσα μέρη, αλλά χρησιμοποιώντας μια πυξίδα, μπορείτε.

Η τέχνη της κατασκευής γεωμετρικών μορφών με τη βοήθεια πυξίδας και χάρακα ήταν ιδιαίτερα ανεπτυγμένη στην αρχαία Ελλάδα. Ένα από τα πιο δύσκολα κατασκευαστικά καθήκοντα, που ήδη ήξεραν πώς να εκτελούν, ήταν η κατασκευή ενός κύκλου εφαπτομένου σε τρεις δεδομένους κύκλους.

Στο σχολείο, μελετούν μια σειρά από τις πιο απλές κατασκευές με πυξίδα και χάρακα (μονόπλευρη χωρίς διαιρέσεις): την κατασκευή μιας ευθείας γραμμής που διέρχεται από ένα δεδομένο σημείο και είναι κάθετη ή παράλληλη σε μια δεδομένη ευθεία. διαίρεση μιας δεδομένης γωνίας στο μισό, διαίρεση ενός τμήματος σε πολλά ίσα μέρη χρησιμοποιώντας το θεώρημα του Θαλή (στην πραγματικότητα, διαίρεση ενός τμήματος με έναν φυσικό αριθμό). κατασκευή τμήματος μεγαλύτερου από το δεδομένο κατά ακέραιο αριθμό φορές (ουσιαστικά πολλαπλασιάζοντας το τμήμα με έναν φυσικό αριθμό). Ωστόσο, ποτέ δεν αντιμετωπίσαμε πρόβλημα όπου θα ήταν απαραίτητο να πολλαπλασιάσουμε ένα τμήμα με ένα τμήμα χρησιμοποιώντας μια πυξίδα και έναν χάρακα, δηλαδή να κατασκευάσουμε ένα τμήμα ίσο με το γινόμενο δύο δεδομένων τμημάτων ή να διαιρέσουμε ένα τμήμα με ένα τμήμα, δηλαδή να κατασκευάσει ένα τμήμα ίσο με τον λόγο των άλλων δύο τμημάτων. Αυτό το πρόβλημα μας φάνηκε πολύ ενδιαφέρον και αποφασίσαμε να το διερευνήσουμε, να προσπαθήσουμε να βρούμε μια λύση και τη δυνατότητα εφαρμογής της μεθόδου της ευρεθείσας λύσης στην επίλυση άλλων προβλημάτων, για παράδειγμα, στα μαθηματικά και τη φυσική.

Κατά την επίλυση κατασκευαστικών προβλημάτων, η παραδοσιακή μεθοδολογία συνιστά τέσσερα στάδια: ανάλυση, κατασκευή, απόδειξη και έρευνα. Ωστόσο, το υποδεικνυόμενο σχήμα για την επίλυση προβλημάτων κατασκευής θεωρείται πολύ ακαδημαϊκό και χρειάζεται πολύς χρόνος για την υλοποίησή του, επομένως, μεμονωμένα στάδια του παραδοσιακού σχήματος για την επίλυση του προβλήματος συχνά παραλείπονται, για παράδειγμα, τα στάδια απόδειξης , έρευνα. Στη δουλειά μας, στο μέτρο του δυνατού, χρησιμοποιήσαμε και τα τέσσερα στάδια, και μάλιστα μόνο όπου υπήρχε ανάγκη και σκοπιμότητα γι' αυτό.

Και το τελευταίο πράγμα: η μέθοδος που βρήκαμε για την κατασκευή των προαναφερθέντων τμημάτων περιλαμβάνει τη χρήση, εκτός από την πυξίδα και τον χάρακα, ενός αυθαίρετα επιλεγμένου μεμονωμένου τμήματος. Η εισαγωγή ενός τμήματος μονάδας υπαγορεύεται επίσης από το γεγονός ότι είναι απαραίτητο τουλάχιστον να επιβεβαιωθεί η εγκυρότητα της μεθόδου που βρήκαμε για την εύρεση ενός τμήματος σε συγκεκριμένα συγκεκριμένα παραδείγματα.

ΓΕΝΙΚΟ ΠΡΟΒΛΗΜΑ Ι

Χρησιμοποιώντας μια πυξίδα και μια ευθεία, κατασκευάστε ένα τμήμα ίσο με το γινόμενο των άλλων δύο τμημάτων.

Σημείωση:

υποτιθεμένος:

Ο κυβερνήτης είναι μονόπλευρος, χωρίς διαχωρισμούς.

Δίνεται τμήμα μοναδιαίου μήκους.

Μελέτη.

1. Θεωρήστε τις ευθείες y=2x-2 2 και y=3x-3 2 και προσπαθήστε να βρείτε τις συντεταγμένες του σημείου τομής αυτών των ευθειών με γεωμετρικές και αναλυτικές μεθόδους:

ένα
) γεωμετρική μέθοδος ( Εικ.1) έδειξε ότι οι συντεταγμένες του σημείου Α της τομής αυτών των ευθειών: «5» είναι η τετμημένη, «6» είναι η τεταγμένη, δηλ. ΑΕ=5, ΑΔ=6.

β) η αναλυτική μέθοδος επιβεβαιώνει αυτό το αποτέλεσμα, δηλ. A (5;6) - το σημείο τομής των γραμμών.

Πράγματι, λύνοντας το σύστημα των εξισώσεων

y=6 А(5;6) - σημείο τομής ευθειών.

2. Θεωρούμε το τμήμα: OB=2, OS=3, AD=6, AE=5.

Μπορεί να υποτεθεί ότι BP=OV×OS, επειδή 6=2×3; AE \u003d OB + OS, επειδή 5=2+3 , όπου

2=ΟΒ-κλίση της εξίσωσης y=2x-2 2 , 3=OS - κλίση της εξίσωσης y=3x-3 2 , AD=y A, OD=x A - συντεταγμένες του σημείου Α της τομής του δικού μας γραμμές.

Θα ελέγξουμε την υπόθεσή μας σε ένα γενικό παράδειγμα με την αναλυτική μέθοδο, δηλ. στις εξισώσεις των ευθειών y=mx-m 2 και y=nx-n 2 (όπου m≠n) ελέγξτε ότι το σημείο τομής των ευθειών έχει συντεταγμένες:

y=nx-n 2 nx-n 2 =mx-m 2 x=(m 2 -n 2)÷(mn)=m+n και y=mx-m 2 =m(m+n)-m 2 = μν

συντεταγμένες του σημείου Α της τομής των ευθειών, όπου m και n είναι οι κλίσεις αυτών των ευθειών κ.λπ.

3. Απομένει να βρεθεί μια μέθοδος για την κατασκευή ενός τμήματος. HELL=OB×OC=m∙n=y A - τεταγμένες του σημείου Α της τομής των ευθειών Y=mx-m 2 και Y=nx-n 2, όπου m≠n και m=OB, n=OC- τμήματα σχεδιάστηκε στον άξονα Ω. Και για αυτό πρέπει να βρούμε μια μέθοδο για την κατασκευή των γραμμών Y=mx-m 2 και Y=nx-n 2 . από τον συλλογισμό είναι σαφές ότι αυτές οι ευθείες πρέπει να διέρχονται από τα σημεία Β και Γ των τμημάτων OB=m και OC=n, που ανήκουν στον άξονα x.

Παρατήρηση 1.Οι παραπάνω χαρακτηρισμοί των τμημάτων αντιστοιχούν στο Σχ. 1 "Παραρτήματα"

Πρώτος τρόποςκατασκευάζοντας ένα τμήμα AD=mn, όπου m>1 μονάδα, n>1 μονάδα, m≠n.

ενιαίο τμήμα

αυθαίρετο τμήμα, m>1ed., n>1ed.

Το n είναι ένα αυθαίρετο τμήμα, όπου m≠n.

Κτίριο (Εικ.2)

Ας τραβήξουμε μια ευθεία γραμμή

Στο OH αναβάλλουμε το OA 1 = Μ

Στο OX αφήνουμε στην άκρη A 1 C 1 \u003d 1 μονάδα

Ας κατασκευάσουμε C 1 B 1 =m, όπου C 1 B 1 ┴ OH

Ας σχεδιάσουμε μια ευθεία γραμμή A 1 B 1, της οποίας η εξίσωση είναι y=mx-m 2 στους άξονες συντεταγμένων XOU (η κλίμακα στους άξονες είναι ίδια).

Σημείωση:

Εικ.2

Παρατήρηση 1.

Πράγματι, η εφαπτομένη της κλίσης αυτής της ευθείας tgά 1 = C 1 B 1 /A 1 C 1 =m/1ed=m, η οποία διέρχεται από το σημείο A 1 του τμήματος OA 1 =m.

Ομοίως, χτίζουμε μια ευθεία γραμμή, η εξίσωση της οποίας είναι Y \u003d nx-n 2.

6. Στον άξονα OX, παραμερίσαμε το OA 2 \u003d n (το σημείο A 2 κατά λάθος συνέπεσε με το σημείο C1).

7. Στον άξονα OX, αφήστε στην άκρη A 2 C 2 \u003d 1 μονάδα.

8. Κατασκευάζουμε B 2 C 2 \u003d n, όπου B 2 C 2 ┴ OH.

9. Ας σχεδιάσουμε μια ευθεία γραμμή B 2 A 2, η εξίσωση της οποίας είναι Y \u003d nx-n 2.

Παρατήρηση 2.Πράγματι, η κλίση αυτής της ευθείας tg ά 2 =C 2 B 2 /A 2 C 2 =n/1ed=n, που διέρχεται από τ. A 2 τμήμα OA 2 =n.

10. Πήραμε t.A (m + n; mn) - το σημείο τομής των γραμμών Y \u003d mx-m 2 και Y \u003d nx-n 2

11. Ας σχεδιάσουμε την ΑΔ κάθετη στο x, όπου η D ανήκει στον άξονα x.

12. Τμήμα AD \u003d mn (τεταγμένη σημείου Α), δηλ. επιθυμητό τμήμα.

Παρατήρηση 3.α) πράγματι, αν στο παράδειγμά μας, n=4 μονάδες, m=3 μονάδες, τότε θα πρέπει να υπάρχουν BP=mn=3 μονάδες∙4 μονάδες=12 μονάδες. Έτσι μας βγήκε: BP = 12 μονάδες? β) η γραμμή B 1 B 2 δεν χρησιμοποιήθηκε σε αυτή την κατασκευή. Στο Β επίσης.

Υπάρχουν τουλάχιστον τρεις διαφορετικοί τρόποι κατασκευής του τμήματος AD=mn.

Δεύτερος τρόπος κατασκευή του τμήματος AD=μν, πουΜ> 1 μονάδα,n> 1 μονάδα,Μκαιn- όποιος.

Ανάλυση

Μια ανάλυση του σχεδίου που κατασκευάστηκε προηγουμένως (Εικ. 2), όπου χρησιμοποιώντας τη μέθοδο που βρέθηκε για την κατασκευή ευθειών Y=mx-m 2 και Y=nx-n 2 βρέθηκε tA (m+n; mn) (αυτή είναι η πρώτη μέθοδος ), προτείνει ότι το mA (m + n; mn) μπορεί να βρεθεί κατασκευάζοντας οποιαδήποτε από αυτές τις γραμμές (U \u003d mx-m 2 ή U \u003d nx-n 2) και την κάθετη AD, όπου η AD είναι η κάθετη στο OX , AD \u003d mn, D ανήκει στον άξονα OH. Τότε το επιθυμητό σημείο Α (m + n, mn) είναι το σημείο τομής οποιασδήποτε από αυτές τις ευθείες και της κάθετης AD. Αρκεί να βρούμε τις γωνίες κλίσης αυτών των ευθειών, οι εφαπτομένες των οποίων, σύμφωνα με τους συντελεστές κλίσης, είναι ίσες με m και n, δηλ. tan ά 1= m και tan ά 2 =n. Λαμβάνοντας υπόψη ότι tg ά 1 =m/1ed=m και tg ά 2 =n/1ed=n, όπου το 1ed είναι ένα μοναδιαίο τμήμα, μπορεί κανείς εύκολα να κατασκευάσει ευθείες των οποίων οι εξισώσεις είναι Y=mx-m 2 και Y=nx-n 2 .

ενιαίο τμήμα

n n>1 μονάδες, τα m και n είναι οποιοιδήποτε αριθμοί.

Π

κατασκευή (Εικ.3)

Εικ.3

1. Ας χαράξουμε μια ευθεία γραμμή ΟΧ.

2. Στον άξονα OX, παραμερίζουμε το τμήμα OA 1 \u003d m.

3. Στον άξονα OX, παραμερίζουμε το τμήμα A 1 D \u003d n.

4. Στον άξονα OX, παραμερίζουμε το τμήμα A 1 C 1 \u003d 1 μονάδα.

5. Χτίζουμε C 1 B 1 \u003d m, όπου C 1 B 1 ┴ OH.

6. Ας σχεδιάσουμε μια ευθεία γραμμή Α1Β1, της οποίας η εξίσωση είναι Y=mx-m2, στους άξονες συντεταγμένων XOU (η κλίμακα στους άξονες είναι ίδια).

7. Επαναφέρετε την κάθετο στην ΟΧ στο σημείο Δ.

8. Λαμβάνουμε το σημείο A (m + n; mn) - το σημείο τομής της ευθείας Y \u003d mx-m2 και της κάθετης AD

9. Τμήμα AD=mn, δηλαδή το επιθυμητό τμήμα.

Συμπέρασμα:Αυτή η δεύτερη μέθοδος είναι πιο καθολική από την πρώτη μέθοδο, καθώς σας επιτρέπει να βρείτε το σημείο A (m + n; mn) και όταν m \u003d n> 1 μονάδα, τότε οι συντεταγμένες αυτού του σημείου είναι A (2m; m 2 ) και AD \u003d m 2.

Με άλλα λόγια, αυτή η μέθοδος σας επιτρέπει να βρείτε ένα τμήμα ίσο με το τετράγωνο του δεδομένου, το μήκος του οποίου είναι μεγαλύτερο από 1 μονάδα.

Σχόλιο:Πράγματι, αν στο παράδειγμά μας m=3 μονάδες, n=5 μονάδες, τότε θα πρέπει να είναι AD=mn=3 μονάδες×5 μονάδες=15 μονάδες. Έτσι το κάναμε: AD=15 μονάδες.

Τρίτος τρόπος κατασκευάζοντας ένα τμήμαΕΝΑ Δ= μν, πουΜ> 1 μονάδα,n> 1 μονάδα καιΜ≠ n.

Χρησιμοποιώντας το σχήμα 2, σχεδιάστε μια διακεκομμένη ευθεία γραμμή B 1 B 2 έως ότου τέμνεται με την OX στο σημείο E € OX, και μια ευθεία γραμμή B 1 B ┴ B 2 C 2, στη συνέχεια

B 1 B \u003d C 1 C 2 \u003d OS 2 -OS 1 \u003d (n + 1 μονάδα) - (m + 1 μονάδα) \u003d nm, και B 2 B \u003d B 2 C 2 -B 1 C 1 \u003d mn => B 1 В=В 2 В=>∆В 1 ВВ 2 - ισοσκελές, ορθογώνιος>∆EC 1 В 1 - ισοσκελές, ορθογώνιος => ά=45º

Επειδή OS 1 \u003d m + 1 μονάδα και EU 1 \u003d B 1 C 1 \u003d m, μετά OE \u003d OS 1 -EC 1 \u003d m + 1 unit-m \u003d 1 μονάδα.

Από το σκεπτικό προκύπτει ότι τα σημεία Β 1 και Β 2 μπορούν να βρεθούν με διαφορετικό τρόπο, γιατί είναι τα σημεία τομής της ευθείας ΕΒ 1 που σύρεται υπό γωνία ά=45º ως προς τον άξονα ΟΧ και κάθετοι στον ΟΧ: В 1 С 1 και В 2 С 2, και ΟΕ=1 μονάδα. Περαιτέρω, χρησιμοποιώντας τις προηγούμενες μεθόδους , θα έχουμε τον παρακάτω τρόπο κατασκευής.

Μονή κοπή.

n n>1 μονάδα και m≠n.

Κατασκευή (Εικ.4)

1. Ας χαράξουμε μια ευθεία γραμμή ΟΧ.

7. Αφήστε κατά μέρος OA 2 \u003d n, όπου A 2 € OX.

8. Αφήστε στην άκρη A 2 C 2 \u003d 1 μονάδα, όπου C 2 € OH.

9. Επαναφέρετε την κάθετο C 2 B 2 στον άξονα OX στο σημείο C 2, όπου B 2 είναι το σημείο τομής της κάθετου με την ευθεία EB 1.

10. Σχεδιάζουμε μια ευθεία A 2 B 2, η εξίσωση της οποίας είναι Y \u003d nx-n 2, έως ότου τέμνεται με την ευθεία A 1 B 1 στο σημείο A.

11. Κατεβάζουμε την κάθετο στην ΟΧ από το σημείο Α και παίρνουμε ΑΔ ίση με mn, όπου Δ € ΟΧ, αφού στα επίπεδα συντεταγμένων των αξόνων ΧΟΥ οι συντεταγμένες του σημείου Α (m + n; mn).

Εικ.4

Σχόλιο:Το μειονέκτημα αυτής της μεθόδου είναι το ίδιο με αυτό της πρώτης μεθόδου κατασκευής, όπου η κατασκευή είναι δυνατή μόνο υπό την προϋπόθεση m≠n.

Τέταρτος τρόπος κατασκευάζοντας ένα τμήμαΕΝΑ Δ= μν, πουΜκαιn- οποιοδήποτε, μεγαλύτερο από ένα τμήμα.

Μονή κοπή.

n n>1 μονάδες, m και n είναι οποιαδήποτε.

Κατασκευή (Εικ.5)

Εικ.5

1. Ας χαράξουμε μια ευθεία γραμμή ΟΧ.

2. Παραμερίστε ΟΕ = 1 μονάδα, όπου Ε € ΟΧ.

3. Πατήστε EC 1 =m, όπου C 1 € OH.

4. Επαναφέρετε την κάθετο στο σημείο C 1 στον άξονα OX.

5. Ας κατασκευάσουμε ά=C 1 EV 1 =45º, όπου B 1 είναι το σημείο τομής της κάθετης C 1 B 1 με την πλευρά ά=45º.

6. Αναβάλλοντας το OA 1 \u003d m, σχεδιάζουμε μια ευθεία γραμμή A 1 B 1, η εξίσωση της οποίας είναι Y \u003d mx-m 2, A € OH.

7. Αφήνουμε στην άκρη A 1 D=n, όπου D € OX.

8. Επαναφέρετε την κάθετο στο σημείο D μέχρι να τέμνεται στο σημείο Α με την ευθεία A 1 B 1, η εξίσωση της οποίας είναι Y \u003d mx-m 2.

9. Τμήμα της κάθετης ΑΔ = το γινόμενο των τμημάτων m και n, δηλαδή ΑΔ = mn, αφού Α (m + n; mn).

Σχόλιο:Αυτή η μέθοδος συγκρίνεται ευνοϊκά με την πρώτη και την τρίτη μέθοδο, όπου m≠n, καθώς έχουμε να κάνουμε με οποιαδήποτε τμήματα m και n, το τμήμα μονάδας μπορεί να είναι μικρότερο από ένα μόνο από αυτά που εμπλέκονται στην αρχή της κατασκευής (έχουμε m> 1 μονάδα).

Γενικό Πρόβλημα II

Χρησιμοποιώντας μια πυξίδα και μια ευθεία, κατασκευάστε ένα ευθύγραμμο τμήμα ίσο με την αναλογία των άλλων δύο ευθύγραμμων τμημάτων.

Σημείωση:

το τμήμα μονάδας είναι μικρότερο από το τμήμα διαιρέτη.

Ο πρώτος τρόπος κατασκευής ενός τμήματοςn= κ/ Μ, πουΜ> 1 μονάδα

Μονή κοπή.

Κτίριο (Εικ.6)

2. Στο ΟΥ παραμερίζουμε ΟΜ = κ.

3. Αφήστε στην άκρη το OA 1 στο OX = Μ.

4. Στο OH, αφήστε στην άκρη A 1 C 1 \u003d 1 μονάδα.

5. Ας φτιάξουμε С 1 В 1 \u003d m, όπου С 1 В 1 ┴ ОХ.

6. Σχεδιάστε μια ευθεία γραμμή A 1 B 1, η εξίσωση της οποίας είναι y=mx-m 2 στους άξονες συντεταγμένων XOU (η κλίμακα στους άξονες είναι ίδια, ίση με 1 μονάδα).

7. Επαναφέρετε την κάθετη ΜΑ στο σημείο Μ στον άξονα ΟΥ, όπου Α είναι το σημείο τομής της ΜΑ με την ευθεία Α 1 Β 1 (δηλαδή Α € Α 1 Β 1).

8. Χαμηλώστε την κάθετο από το σημείο Α στον άξονα ΟΧ μέχρι να τέμνεται με τον άξονα ΟΧ στο σημείο Δ. Το τμήμα ΑΔ=ΟΜ=κ=μν.

9. Τμήμα A 1 D \u003d n - το επιθυμητό τμήμα, ίσο με n \u003d k / m.

R Εικ.6

Απόδειξη:

1. Η εξίσωση της ευθείας A 1 B 1 είναι πραγματικά Y=mx-m 2, στο Y=0 έχουμε 0=mx-m 2 => x=m=OA 1, και η κλίση είναι tg

2. Σε ∆ADA 1 tg 1 D=AD/A 1 D=B 1 C 1 /A 1 C 1 =>A 1 D=AD×A 1 C 1 /B 1 C 1 =k×1μονάδα/m= mn /m=n, δηλ Και 1 D=n=k/m είναι το επιθυμητό τμήμα.

Σχόλιο.Πράγματι, αν στο παράδειγμά μας m=3 μονάδες, k=15 μονάδες, τότε θα πρέπει να είναι A 1 D=n=k/m=15 μονάδες/3 μονάδες=5 μονάδες. Κάναμε ακριβώς αυτό.

Δεύτερος τρόπος κατασκευάζοντας ένα τμήμαn= κ/ Μ, πουΜ> 1 μονάδα

Μονή κοπή.

Εικ.7

1. Κατασκευάζουμε τους άξονες συντεταγμένων XOU.

2. Στο ΟΥ παραμερίζουμε ΟΜ = κ.

3. Αφήστε κατά μέρος ΟΕ \u003d 1 μονάδα, όπου E € OX.

4. Αφήστε κατά μέρος EC 1 \u003d m, όπου C 1 € OX.

5. Επαναφέρετε την κάθετο στο σημείο C 1 στον άξονα OX.

6. Κατασκευάζουμε C 1 EB 1 \u003d 45º, όπου B 1 είναι το σημείο τομής της κάθετης C 1 B 1 με την πλευρά της γωνίας C 1 EB 1 \u003d 45º.

7. Αφήστε στην άκρη το OA 1 στο OX = Μ.

8. Σχεδιάστε μια ευθεία γραμμή A 1 B 1, η εξίσωση της οποίας είναι y=mx-m 2 στους άξονες συντεταγμένων XOU (η κλίμακα στους άξονες είναι ίδια, ίση με 1 μονάδα).

9. Επαναφέρετε την κάθετη ΜΑ στο σημείο Μ στον άξονα ΟΥ, όπου Α είναι το σημείο τομής της ΜΑ με την ευθεία Α 1 Β 1 (δηλαδή Α € Α 1 Β 1).

10. Χαμηλώστε την κάθετο από το σημείο Α στον άξονα ΟΧ έως ότου τέμνεται με τον άξονα ΟΧ στο σημείο Δ. Το τμήμα ΑΔ=ΟΜ=k=mn.

11. Τμήμα A 1 D=n - το επιθυμητό τμήμα, ίσο με n=k/m.

Απόδειξη:

1.∆B 1 C 1 E - ορθογώνιο και ισοσκελές, αφού C 1 EB 1 \u003d 45º \u003d\u003e B 1 C 1 \u003d EU 1 \u003d m.

2.A 1 C 1 \u003d OS 1 - OA 1 \u003d (OE + EC1) - OA 1 \u003d 1 μονάδα + m-m \u003d 1 μονάδα.

3. Η εξίσωση της ευθείας A 1 B 1 είναι πραγματικά Y=mx-m 2, στο Y=0 έχουμε 0=mx-m 2 => x=m=OA 1, και η κλίση είναι tg

4.V ∆ADA 1 tg 1 D=AD/A 1 D=B 1 C 1 /A 1 C 1 => A 1 D=AD×A 1 C 1 /B 1 C 1 =k ×1 μονάδα/m= mn/m=n, δηλ Και 1 D=n=k/m είναι το επιθυμητό τμήμα.

συμπέρασμα

Στην εργασία μας, βρήκαμε και μελετήσαμε διάφορες μεθόδους για την κατασκευή ενός τμήματος ίσου με το γινόμενο ή την αναλογία δύο άλλων τμημάτων χρησιμοποιώντας πυξίδα και χάρακα, έχοντας προηγουμένως δώσει τον δικό μας ορισμό αυτών των πράξεων με τμήματα, αφού δεν μπορούσαμε να βρούμε σε κανένα ειδική βιβλιογραφία όχι μόνο ο ορισμός του πολλαπλασιασμού και της διαίρεσης τμημάτων, αλλά ακόμη και η αναφορά αυτών των πράξεων σε τμήματα.

Εδώ έχουμε χρησιμοποιήσει σχεδόν και τα τέσσερα στάδια: ανάλυση, κατασκευή, απόδειξη και έρευνα.

Συμπερασματικά, θα θέλαμε να σημειώσουμε τη δυνατότητα χρήσης των μεθόδων που βρέθηκαν για την κατασκευή τμημάτων σε ορισμένους κλάδους της φυσικής και των μαθηματικών.

1. Εάν επεκτείνετε τις ευθείες y=mx-m 2 και y=nx-n 2 (n>m>0) έως ότου τέμνονται με τον άξονα OS, τότε μπορείτε να πάρετε τμήματα ίσα με m 2, n 2, n 2 - m 2 (Εικ.8), όπου ΟΚ \u003d m 2, OM \u003d n 2, KM \u003d n 2 - m 2.

R
Εικ.8

Απόδειξη:

Αν x=0, τότε y=0-m 2 => OK=m 2 .

Ομοίως, αποδεικνύεται ότι OM= n 2 =>KM=OM-OK= n 2 - m 2 .

2. Δεδομένου ότι το γινόμενο δύο τμημάτων είναι το εμβαδόν ενός ορθογωνίου με πλευρές ίσες με αυτά τα τμήματα, τότε, έχοντας βρει ένα τμήμα ίσο με το γινόμενο των άλλων δύο, αντιπροσωπεύουμε έτσι το εμβαδόν του ορθογωνίου στο μορφή τμήματος του οποίου το μήκος είναι αριθμητικά ίσο με αυτό το εμβαδόν.

3. Στη μηχανική, τη θερμοδυναμική, υπάρχουν φυσικά μεγέθη, για παράδειγμα, έργο (Α=FS, A=PV), αριθμητικά ίσα με τα εμβαδά των ορθογωνίων που είναι κατασκευασμένα στα αντίστοιχα επίπεδα συντεταγμένων, επομένως, σε εργασίες όπου, για παράδειγμα, απαιτείται η σύγκριση της εργασίας με τα εμβαδά των ορθογωνίων, είναι πολύ απλό να γίνει αυτό εάν αυτές οι περιοχές αντιπροσωπεύονται ως τμήματα αριθμητικά ίσα με τα εμβαδά των ορθογωνίων. Και τα τμήματα είναι εύκολο να συγκριθούν μεταξύ τους.

4. Η εξεταζόμενη μέθοδος κατασκευής σάς επιτρέπει να δημιουργήσετε άλλα τμήματα, για παράδειγμα, χρησιμοποιώντας το σύστημα εξισώσεων y=mx-m 3 και y=nx-n 3 , μπορείτε να δημιουργήσετε τμήματα με δεδομένα m και n όπως m 2 +mn +n 2 και mn(m+n), αφού το σημείο Α της τομής των ευθειών που δίνεται από αυτό το σύστημα εξισώσεων έχει συντεταγμένες (m 2 +mn+n 2; mn(m+n), και μπορείτε επίσης να κατασκευάσετε τμήματα n 3 , m 3, και η διαφορά n 3 - m 3 που προκύπτει στο OS στην αρνητική περιοχή στο X=0.

Εργα ΤΕΧΝΗΣ. ... βοήθεια πυξίδακαι κυβερνώντες. Αλγόριθμος διαίρεσης τμήμαΑΒ στη μέση: 1) βάλε το πόδι πυξίδαστο σημείο Α· 2) τοποθετήστε κονίαμα πυξίδα ίσοςμήκος τμήμα ...

Βιογραφία του Πυθαγόρα

Βιογραφία >> Μαθηματικά

... Κτίριοκανονικά γεωμετρικά σχήματα βοήθεια πυξίδακαι κυβερνώντες. ... βοήθεια πυξίδακαι κυβερνώντες. Περισσότερο από δύο ... είναι ίσο με b/4+p, το ένα πόδι είναι ίσο με b/4, και αλλοβ/2-π. Με το Πυθαγόρειο θεώρημα έχουμε: (b/4+p)=(b/4)+(b/4-p) ή ...

Εάν είναι απολύτως φυσικό ότι, με την υπόθεση μεγαλύτερης ποικιλίας εργαλείων, αποδεικνύεται ότι είναι δυνατή η επίλυση μεγαλύτερου συνόλου κατασκευαστικών προβλημάτων, τότε θα μπορούσε κανείς να προβλέψει ότι, αντίθετα, υπό τους περιορισμούς που επιβάλλονται στα εργαλεία, η κατηγορία των επιλύσιμων προβλημάτων θα περιοριστεί. Ακόμη πιο αξιοσημείωτη είναι η ανακάλυψη που έκανε ο Ιταλός Mascheroni (1750-1800):Όλες οι γεωμετρικές κατασκευές που μπορούν να γίνουν με πυξίδα και ευθύγραμμο μπορούν να γίνουν με μία μόνο πυξίδα.Θα πρέπει, φυσικά, να οριστεί ότι είναι στην πραγματικότητα αδύνατο να τραβήξουμε μια ευθεία γραμμή μέσω δύο δεδομένων σημείων χωρίς χάρακα, επομένως αυτή η βασική κατασκευή δεν καλύπτεται από τη θεωρία του Mascheroni. Αντίθετα, πρέπει να υποθέσει κανείς ότι μια ευθεία δίνεται εάν δίδονται δύο από τα σημεία της. Αλλά μόνο με τη βοήθεια μιας πυξίδας, είναι δυνατό να βρεθεί το σημείο τομής δύο ευθειών που δίνονται με αυτόν τον τρόπο ή το σημείο τομής μιας ευθείας με έναν κύκλο.

Πιθανώς το απλούστερο παράδειγμα κατασκευής του Mascheroni είναι ο διπλασιασμός ενός δεδομένου τμήματος ΑΒ. Η λύση έχει ήδη δοθεί στις σ. 174-175. Επιπλέον, στις σελίδες 175-176, μάθαμε πώς να διαιρούμε αυτό το τμήμα στη μέση. Ας δούμε τώρα πώς διχοτομούμε το τόξο ενός κύκλου ΑΒ με κέντρο το Ο. Ακολουθεί μια περιγραφή αυτής της κατασκευής (Εικ. 47). Με την ακτίνα AO σχεδιάζουμε δύο τόξα με κέντρα Α και Β. Από το σημείο Ο αφήνουμε σε αυτά τα τόξα δύο τέτοια τόξα OP και OQ που OP = OQ = AB. Στη συνέχεια βρίσκουμε το σημείο τομής R του τόξου με κέντρο P και ακτίνα PB και το τόξο με κέντρο Q και ακτίνα QA. Τέλος, λαμβάνοντας το τμήμα OR ως ακτίνα, περιγράφουμε το τόξο με το κέντρο P ή Q μέχρι την τομή με το τόξο AB - το σημείο τομής είναι το επιθυμητό μέσο του τόξου AB. Αφήνουμε την απόδειξη στον αναγνώστη ως άσκηση.

Θα ήταν αδύνατο να αποδειχθεί ο κύριος ισχυρισμός του Mascheroni δείχνοντας, για κάθε κατασκευή που μπορεί να γίνει με πυξίδα και ευθεία, πώς μπορεί να γίνει με μία μόνο πυξίδα: τελικά, υπάρχει άπειρος αριθμός πιθανών κατασκευών. Αλλά θα επιτύχουμε τον ίδιο στόχο εάν προσδιορίσουμε ότι καθεμία από τις ακόλουθες βασικές κατασκευές είναι εφικτή με μία μόνο πυξίδα:

1. Σχεδιάστε έναν κύκλο αν δίνεται το κέντρο και η ακτίνα του.
2. Βρείτε τα σημεία τομής δύο κύκλων.
3. Βρείτε τα σημεία τομής της ευθείας και του κύκλου.
4. Βρείτε το σημείο τομής δύο ευθειών.

Οποιαδήποτε γεωμετρική κατασκευή (με τη συνήθη έννοια, με την υπόθεση πυξίδας και ευθύγραμμης γραμμής) αποτελείται από μια πεπερασμένη ακολουθία αυτών των στοιχειωδών κατασκευών. Το ότι τα δύο πρώτα από αυτά είναι εφικτά με μία μόνο πυξίδα είναι αμέσως ξεκάθαρο. Οι πιο δύσκολες κατασκευές 3 και 4 εκτελούνται χρησιμοποιώντας τις ιδιότητες αντιστροφής που συζητήθηκαν στην προηγούμενη παράγραφο.

Ας στραφούμε στην κατασκευή 3: βρείτε τα σημεία τομής ενός δεδομένου κύκλου C με μια ευθεία που διέρχεται από τα δεδομένα σημεία Α και Β. Σχεδιάστε τόξα με κέντρα Α και Β και ακτίνες ίσες με AO και BO, αντίστοιχα, εκτός από το σημείο O, τέμνονται στο σημείο P. Στη συνέχεια κατασκευάζουμε το σημείο Q, αντίστροφο προς το σημείο P ως προς τον κύκλο C (δείτε την κατασκευή που περιγράφεται στη σελίδα 174). Τέλος, σχεδιάζουμε έναν κύκλο με κέντρο Q και ακτίνα QO (σίγουρα θα τέμνεται με το C): τα σημεία τομής του X και X "από τον κύκλο C και θα είναι τα επιθυμητά. Για να το αποδείξουμε, αρκεί να διαπιστωθεί ότι καθένα από τα σημεία Χ και Χ» βρίσκεται στην ίδια απόσταση από το Ο και το Ρ (όσον αφορά τα σημεία Α και Β, η ανάλογη ιδιότητά τους προκύπτει αμέσως από την κατασκευή). Πράγματι, αρκεί να αναφερθούμε στο γεγονός ότι το αντίστροφο προς το σημείο Q σημείο χωρίζεται από τα σημεία Χ και Χ «από απόσταση ίση με την ακτίνα του κύκλου C (βλ. σελ. 173). Αξίζει να σημειωθεί ότι το κύκλος που διέρχεται από τα σημεία Χ, Χ" και Ο, είναι η αντίστροφη ευθεία ΑΒ σε αντιστροφή ως προς τον κύκλο Γ, αφού αυτός ο κύκλος και η ευθεία ΑΒ τέμνουν την Γ στα ίδια σημεία. (Όταν είναι ανεστραμμένα, τα σημεία του βασικού κύκλου παραμένουν σταθερά.) Αυτή η κατασκευή είναι αδύνατη μόνο εάν η ευθεία ΑΒ διέρχεται από το κέντρο C. Αλλά τότε τα σημεία τομής μπορούν να βρεθούν από την κατασκευή που περιγράφεται στη σελ. 178, όπως τα μέσα του τα τόξα C, που λαμβάνονται όταν σχεδιάζουμε έναν αυθαίρετο κύκλο με κέντρο Β, που τέμνεται με το C στα σημεία B 1 και B 2.

Η μέθοδος σχεδίασης κύκλου αντίστροφου σε ευθεία γραμμή, «συνδέοντας δύο δεδομένα σημεία, δίνει αμέσως μια κατασκευή που λύνει το πρόβλημα 4. Έστω οι ευθείες που δίνονται από τα σημεία Α, Β και Α», Β» (Εικ. 50) Ας σχεδιάσουμε έναν αυθαίρετο κύκλο Γ και χρησιμοποιώντας την παραπάνω μέθοδο ας κατασκευάσουμε κύκλους αντίστροφους προς τις ευθείες ΑΒ και ΑΒ "Β". Αυτοί οι κύκλοι τέμνονται στο σημείο Ο και σε άλλο σημείο Υ, το σημείο Χ, το αντίστροφο του σημείου Υ, είναι το επιθυμητό σημείο τομής: Ο τρόπος κατασκευής του έχει ήδη εξηγηθεί παραπάνω. Ποιο X είναι το επιθυμητό σημείο, αυτό είναι ξεκάθαρο από το γεγονός ότι το Y είναι το μόνο σημείο αντίστροφο σε ένα σημείο που ανήκει ταυτόχρονα και στις δύο ευθείες AB και A "B", επομένως, το σημείο Το X, το αντίστροφο του Y, πρέπει να βρίσκεται ταυτόχρονα στο AB και στο A "B" .

Αυτές οι δύο κατασκευές συμπληρώνουν την απόδειξη της ισοδυναμίας μεταξύ των κατασκευών του Mascheroni, στις οποίες επιτρέπονται μόνο πυξίδες, και των συνηθισμένων γεωμετρικών κατασκευών με πυξίδες και ευθεία.

Δεν μας ένοιαζε η κομψότητα της επίλυσης των επιμέρους προβλημάτων που εξετάσαμε εδώ, αφού στόχος μας ήταν να ξεκαθαρίσουμε το εσωτερικό νόημα των κατασκευών του Mascheroni. Αλλά ως παράδειγμα, θα αναφέρουμε επίσης την κατασκευή ενός κανονικού πενταγώνου. Πιο συγκεκριμένα, μιλάμε για την εύρεση περίπου πέντε σημείων σε έναν κύκλο που μπορούν να χρησιμεύσουν ως κορυφές ενός κανονικού εγγεγραμμένου πενταγώνου.

Έστω Α ένα αυθαίρετο σημείο στον κύκλο Κ. Δεδομένου ότι η πλευρά ενός κανονικού εγγεγραμμένου εξαγώνου είναι ίση με την ακτίνα του κύκλου, δεν θα είναι δύσκολο να βάλουμε στο K τέτοια σημεία B, C, D που AB \u003d BC \ u003d CD \u003d 60 ° (Εικ. 51). Σχεδιάζουμε τόξα με κέντρα A και D με ακτίνα ίση με AC. ας τέμνονται στο σημείο Χ. Τότε, αν το Ο είναι το κέντρο του Κ, το τόξο με κέντρο Α και ακτίνα ΟΧ θα τέμνει το Κ στο σημείο F, που είναι το μέσο του τόξου BC (βλ. σελ. 178). Στη συνέχεια, με ακτίνα ίση με την ακτίνα K, περιγράφουμε τόξα με κέντρο F που τέμνεται με το K στα σημεία G και H. Έστω Y ένα σημείο του οποίου οι αποστάσεις από τα σημεία G και H είναι ίσες με OX και το οποίο χωρίζεται από το X κατά κέντρο Ο. Στην περίπτωση αυτή, το τμήμα AY ως φορές είναι η πλευρά του επιθυμητού πενταγώνου. Η απόδειξη αφήνεται στον αναγνώστη ως άσκηση. Είναι ενδιαφέρον να σημειωθεί ότι στην κατασκευή χρησιμοποιούνται μόνο τρεις διαφορετικές ακτίνες.

Το 1928, ο Δανός μαθηματικός Hjelmslev βρήκε ένα αντίγραφο ενός βιβλίου σε ένα βιβλιοπωλείο στην Κοπεγχάγη που ονομάζεται Ευκλείδης Δανικός, που εκδόθηκε το 1672 από άγνωστο συγγραφέα G. Περισσότερα.Από τη σελίδα του τίτλου, θα μπορούσε κανείς να συμπεράνει ότι αυτή ήταν μόνο μια από τις παραλλαγές των Ευκλείδειων «Αρχών», που παρέχεται, ίσως, με σχόλιο ενός εκδότη. Αλλά σε πιο προσεκτική εξέταση, αποδείχθηκε ότι περιείχε μια πλήρη λύση στο πρόβλημα Mascheroni, που βρέθηκε πολύ πριν από Mascheroni.

Γυμνάσια. Στη συνέχεια γίνεται περιγραφή των κατασκευών του Mohr. Ελέγξτε αν είναι σωστές. Γιατί μπορεί να υποστηριχθεί ότι λύνουν το πρόβλημα Mascheroni;

Εμπνευσμένο από τα αποτελέσματα του Mascheroni, Jacob Steiner (1796-1863)έκανε μια προσπάθεια να μελετήσει κατασκευές που μπορούν να γίνουν μόνο με τη βοήθεια ενός χάρακα. Φυσικά, ο χάρακας από μόνος του δεν οδηγεί πέρα ​​από το δεδομένο αριθμητικό πεδίο και επομένως δεν αρκεί να εκτελεστούν όλες οι γεωμετρικές κατασκευές με την κλασική τους έννοια. Αλλά ακόμη πιο αξιοσημείωτα είναι τα αποτελέσματα που έλαβε ο Στάινερ με τον περιορισμό που εισήγαγε - να χρησιμοποιήσει την πυξίδα μόνο μία φορά. Απέδειξε ότι όλες οι κατασκευές στο επίπεδο που μπορούν να γίνουν με πυξίδα και χάρακα μπορούν επίσης να γίνουν με έναν μόνο χάρακα, με την προϋπόθεση ότι δίνεται ένας μόνο σταθερός κύκλος μαζί με το κέντρο. Αυτές οι κατασκευές περιλαμβάνουν τη χρήση προβολικών μεθόδων και θα περιγραφούν στη συνέχεια (βλ. σελ. 228).

* Χωρίς κύκλο, και, επιπλέον, με κέντρο, είναι αδύνατο να γίνει. Για παράδειγμα, εάν δίνεται ένας κύκλος, αλλά το κέντρο του δεν έχει καθοριστεί, τότε είναι αδύνατο να βρεθεί το κέντρο χρησιμοποιώντας έναν μόνο χάρακα. Θα το αποδείξουμε τώρα, ωστόσο, αναφερόμενοι, ωστόσο, στο γεγονός που θα διαπιστωθεί αργότερα (βλ. σελ. 252): υπάρχει τέτοια μετατροπή του επιπέδου στον εαυτό του που α) ο δεδομένος κύκλος παραμένει σταθερός, β) κάθε ευθεία η γραμμή περνά σε ευθεία γραμμή, με ) το κέντρο ενός σταθερού κύκλου δεν παραμένει σταθερό, αλλά μετατοπίζεται. Η ίδια η ύπαρξη ενός τέτοιου μετασχηματισμού δείχνει την αδυναμία κατασκευής του κέντρου ενός δεδομένου κύκλου χρησιμοποιώντας έναν μόνο χάρακα. Πράγματι, όποια και αν είναι η διαδικασία κατασκευής, καταλήγει σε μια σειρά ξεχωριστών βημάτων που συνίστανται στη χάραξη ευθειών γραμμών και στην εύρεση των τομών τους μεταξύ τους ή με έναν δεδομένο κύκλο. Φανταστείτε τώρα ότι ολόκληρο το σχήμα στο σύνολό του είναι ένας κύκλος και όλες οι ευθείες γραμμές που χαράσσονται κατά μήκος του χάρακα κατά την κατασκευή του κέντρου υπόκεινται στον μετασχηματισμό, την ύπαρξη του οποίου επιτρέψαμε εδώ. Τότε είναι σαφές ότι το σχήμα που προκύπτει μετά τον μετασχηματισμό θα ικανοποιούσε επίσης όλες τις απαιτήσεις της κατασκευής. αλλά η κατασκευή που υποδεικνύεται από αυτό το σχήμα θα οδηγούσε σε ένα σημείο διαφορετικό από το κέντρο του δεδομένου κύκλου. Ως εκ τούτου, η εν λόγω κατασκευή είναι αδύνατη.